University of Cambridge > Mathematics > Statistical Laboratory > Richard Weber > Optimization and Control

Optimization and Control

Broom balancing as a control problem

This is home page for the course of 16 lectures for third year Cambridge mathematics students. It was last given in autumn 2010. It will next be given starting January 19, 2012 (Tue/Thu @ 9am in CMS meeting room 3).

If you are interested in receiving an email alert when this course is updated you can subscribe to the comments thread below.

This material is provided for students, supervisors (and others) to freely use in connection with this course. Copyright remains with the author. Notice to external persons accessing this page

Feedback

This year's course is almost over and will finish on 13 March 2012. You can give feedback on-line here. This will be sent to my email anonymously. After reading the responses, I will forward them to the Faculty Office. 8 students have sent feedback thus far.

Introduction

This is a course on optimization problems that are posed over time. It is helpful to be familiar with some ideas that have been introduced in prior courses in Optimization, Probability and Markov Chains. However, you should not worry if you did not attend these courses, as there is really nothing you will need to know that cannot be picked up along the way.

Importantly we now add dynamic and stochastic elements that were not present in that course, and consider what happens when some variables are imperfectly observed. Applications of this course are to be found in science, economics and engineering (e.g., "insects as optimizers", "planning for retirement", "finding a parking space", "optimal gambling" and "steering a space craft to the moon"). The course should appeal to those who liked the type of problems occurring in Optimization IB, Markov Chains IB and Probability IA.

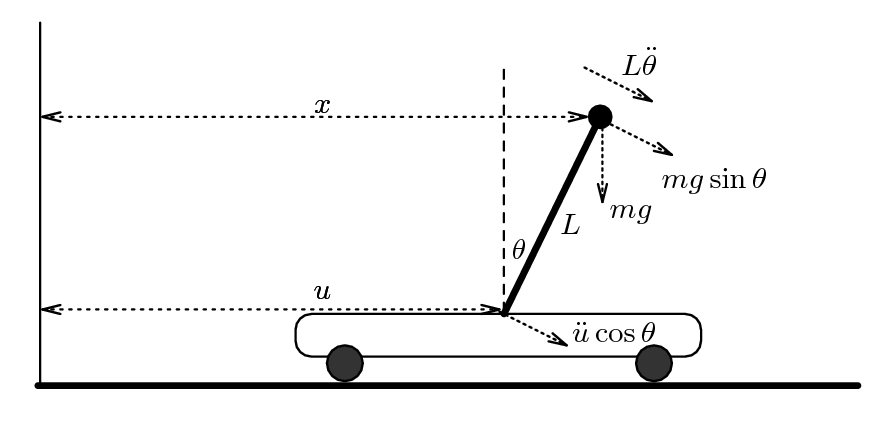
The diagram of the trolley on wheels at the top of this page models the problem that a juggler has when she tries to balance a broom upright in one hand. In this course you will learn how to balance N brooms simultaneously, on top of one another, or perhaps side by side. Can you guess which of these two juggling trick is more difficult?

Course notes

I aim to make each lecture a self-contained unit on a topic, with notes of four A4 pages. 

Here are the course notes 2012. They are now complete.

• Table of contents
• Lectures 1–16
• Slides used in Lecture 6: Multi-armed bandits and Gittins index
• Index
  

These note include hyperlinks between references to equations and to keywords in the index, but those may not be visible within your browser, only if you download the notes.

Here also are course notes for 2010-11. The notes for this year will be an incrementally improved version of these.

Course Blog

There is a course blog in which I will make a few comments after each lecture: to emphasize an idea, give a sidebar, correction (!), or answer an interesting question (that perhaps a student sends to me in email).

Example Sheets

There are 3 examples sheets, each containing 11 questions, in this single file: exsheetoc.pdf. You should receive a supervision on each examples sheet. 

The examples that were set for the 2010 course are in this single file: exsheet2010.pdf. I have made some small changes in preparing the sheets for the 2012 course.

Example Sheets Solutions

Worked solutions to the questions on the example sheets can be obtained by persons (such as supervisors) with a bona fide reason by sending email to me (rrw1@cam.ac.uk).

Recommended books

1. Bertsekas, D. P., Dynamic Programming. Prentice Hall, 1987. (Useful for Part I of the course.)
2. Bertsekas, D. P., Dynamic Programming and Optimal Control, Volumes I and II, Prentice Hall, 1995. (Useful for all parts of the course.)
3. Hocking, L. M., Optimal Control: An introduction to the theory and applications, Oxford 1991. (Chapters 4-7 are good for Part III of the course.)
4. Ross, S., Introduction to Stochastic Dynamic Programming. Academic Press, 1983. (Chapters I-V are useful for Part I of the course.)
5. Whittle, P., Optimization Over Time. Volumes I and II. Wiley, 1982-83. (Chapters 5, 17 and 18 of volume I are useful for Part II of the course. Chapter 7, volume II is good for Part III of the course.)

Exam questions

Here is a file of all tripos questions in Optimization and Control for 2001-2011.

Here are past tripos questions 1995-2006: tripos.pdf

Some of these questions have amusing real-life applications.

A comment on making good use of a lecturer's printed notes

I sometimes wonder whether it is helpful to publish full course notes. It is helpful that we can dispense with some tedious copying-out, and you are guaranteed an accurate account. But there are also benefits to hearing and writing down things yourself during a lecture, and so I hope you will still do some of that. I intend to say some things in every lecture that are not in the notes. In learning mathematics repeated exposure to ideas is helpful, so I hope that a combination of reading, listening, writing and solving problems will work well for you. I would be interested to hear from you if you would like to tell me what you think about this, and how you find best to use the notes that I am putting here.

Digressions

I have some years included a small digression half way through each lecture. Here are some of the overheads I have used for these in the past. However, I am thinking I will omit these in 2012 and focus only on the course..

1. The prisoners' dilemma with repetition and discounting (lecture 3).
2. The `find the oldest' problem (lecture 4).
3. The Palasti conjecture, a parking problem (lecture 5).
4. A self-organizing system (lecture 6).
5. A repeated game with hidden knowledge (lecture 7).
6. Black Magic, 9 to 5 (photocopiers, Lecture 8).
7. Instability of a random access communication channel (aloha, Lecture 9).
8. Optimal search for a moving target (lecture 10).
9. The lady's nylon stocking problem (Lecture 12).
10. An advertising model.

Other resources and further reading

Here is what the Occupational Outlook Handbook says about careers in operations research.

Here is the home page of INFORMS, the Institute for Operations Research and the Management Sciences.

Here is the home page of the UK Operational Research Society.

Please send me email with comments or corrections on my lectures, the notes or the examples sheet. I am very glad to receive comments and suggestions from students studyng the course.