Markov Chains · Course Blog
This is the blog page for my course of 12 lectures to second year Cambridge mathematics students in autumn 2011. This material is provided for students, supervisors (and others) to
freely use in connection with this course.
I intend to make a few comments after each lecture: to
emphasize an idea, give a sidebar, correction (!), or answer an interesting
question (that perhaps a student sends to me in email).
Lecture 12
The last lecture was on Tuesday November 15. I have enjoyed giving this course and I hope you have enjoyed it too.
The notes are now finalized and probably safe for you to download as a final version. I made a change to page 48 around 9am today. If there are any more changes then I will put a remark on the course page. You can now also look at the overhead projector slides that I sometimes used in lectures, such as those today that I used to summarise four Part II courses that you may like to study next year.
Some students say that the notation is one of the most difficult things about this course. I recommend that you make for yourself a one-page crib sheet of all the notation:
(Xn)n≥0, I, Markov(λ,P), P = (pij), P(n) = (pij(n)), hiA, kiA, Hi, Ti, Vi, Vi(n), fi, λ, π, γik, mi .
Write a little explanation for yourself as to what each notation means, and how it used in our theorems about right-hand equations, recurrence/transience, left-hand equations, existence/uniqueness of invariant measure, aperiodicity/periodicity, positive/null recurrence and detailed balance. It should all seems pretty straightforward and memorable once you summarise it on one page and make some notes to place it in context.
Of course I could easily typeset a page like this for you — but I think that you'll learn more, and it will be more memorable for you personally, if you create this crib sheet yourself!
In my discussion of random walk and electrical networks in Section 12.4 I appealed to Rayleigh's Monotonicity Law: " if some resistances of a circuit are increased (decreased) the resistance between any two points of the circuit can only increase (decrease)." A proof of this "obvious" fact can be constructed by (i) proving Thomson's Principle: "Flows determined by Kirchhoff's Laws minimize energy dissipation", and then (ii) showing that Thomson's Principle implies Rayleigh's Monotonicity Law. You can read the details of this in Doyle and Snell Random walks and electric networks, pages 51–52.
In Section 12.2 I mentioned Burke's output theorem (1956) which says that the output process of a M/M/1 queue in equilibrium is a Poisson process with the same rate as the input. In writing "M/M/1" the "M"s mean Markovian (i.e. a Poisson input process of rate λ and i.i.d. exponentially distributed service times with parameter μ (where μ>λ), and the "1" means a single server. In queueing theory this very useful notation is known as Kendall's notation.)
I remarked (just for fun) that queueing is the only common word in the OED with five vowels in a row. Obscure words are ones like "miaoued" (what the cat did).
I once proved a generalization of Burke's output theorem that holds even when the queue has not reached equilibrium (see: The interchangeability of ·/M/1 queues in series, Weber, 1979). Suppose we have two single-server queues in series, which we might write as /M/1 → /M/1. The customers' service times in the first queue are i.i.d. exponentially distributed with parameter λ and in the second queue they are i.i.d. exponentially distributed with parameter μ. On finishing service in the first queue a customer immediately joins the second queue. Suppose the system starts with N cusomers in the first (upstream) queue and no customers in the second (downstream) queue. My theorem says that all statistics that we might measure about the departure process from the second queue are the same if λ and μ are interchanged. Thus by observing the process of departures from the second queue we cannot figure out which way around the two /M/1 servers are ordered. For example, the time at which we see the first departure leave the second queue has expected value 1/λ + 1/μ (which is symmetric in λ and μ). All other statistics are also symmetric in λ and μ. Burke's theorem is a corollary of this that can be obtained by thinking about N tending to infinity (can you see how?)
Further Reading
To consolidate your learning it would be helpful to browse at least one alternative text that covers the same ground as my lecture notes (and James Norris's book Chapter 1). You will recognize things that you already know, but because they are presented a bit differently this should get you thinking about whether you really understand the concepts. I recommend chapters in books by Grimmett, and by Ross, and notes you can access online by Konstantopoulos (Chapters 1–32), Grimstead and Snell (Chapter 11), and (for those of you who thought the course was too easy and would like to read something more intellectually stretching) Levin, Peres and Wilmer (Chapters 1 and 2) or Aldous and Fill (Chapters 1–3).Lecture 11
I started the lecture by mentioning the second law of thermodynamics, which says that entropy is a nondecreasing function of time.
For a distribution p=(p1, ..., pk) the entropy, H(p) = –sum_i p_i log(p_i), is a measure of disorder, or how surprising on average would be an outcome that is chosen according to this distribution. For example, the outcome of the toss of a biased coin is less surprising on average than the outcome of a toss of a fair coin, and this is expressed by the inequality
– p log p – (1–p) log(1–p) ≤ – (1/2) log(1/2) – (1/2) log(1/2).
When the log is taken base 2 then H(p) is a lower bound on the average number of binary bits that would be required to communicate an outcome that is chosen as one of k possible outcomes according to this distribution. The bound can be achieved if and only if every component of p is one of 1/2, 1/4, 1/8, ... . If that is not the case then we might consider taking m i.i.d. samples from this distribution, and then try to communicate these m results optimally as one block. There exists a coding that does this and needs only m·H(p) bits, asymptotically as as m tends to infinity.
I gave an example of a 4 state Markov chain which starts in state 1, and thus having entropy H((1,0,0,0))=0. As n increases the distribution given by the first row of P^n tends to (1/4,1/4/,1/4,1/4), and the entropy increases monotonically to 2 (using log base 2). The point of this example was to motivate the idea that reversibility is only going to make sense once our Markov chain has reached its equilibrium. Otherwise the process will look different when reversed in time because it will appear that entropy is decreasing.
In fact, I cheated a little here, because it is not always the case that the entropy of p_1^{(n)}=(p_{1j}^{(n)}, j=1, ....,k) is monotonically increasing in n. This is true if and only if the equilibrium distribution of the Markov chain is the uniform distribution (as it was in my example). Nonetheless the same point is valid. Unless we start the chain in equilibrium we will be able to detect some difference between the process run forward in time and the process run backwards in time.
There is a Part II course called Coding and Cryptography in which you can learn more about entropy as it relates to efficient communications. Not surprisingly, it also crops up in the Cosmology and Statistical Physics courses.
Following the lecture I made a change in the notes to the proof of Theorem 11.4, and a small correction in Example 11.5.
Lecture 10
We only proved the first part of Theorem 10.2 (Ergodic theorem). The second part is a simple corollary of the first part. For details you can look at page 3 in Section 1.10 of Jame's Norris's notes.
The material on the random target lemma and Kemeny's constant is non-examinable, but I have presented because I think it is fun. It is surprising (don't you think?) that the expected time to reach equilibrium (in the sense of this lemma) is independent of the starting state. (As well being a co-author with Laurie Snell of the book Finite Markov Chains, John Kemeny was President of Dartmouth College, and one of the inventors of the BASIC programming language.)
Of course there are other ways to think about the time that is required for a Markov chain to reach equilibrium. One is the mixing time, τ(ε), which is defined for ε>0 as the the least time such that
maxi ∑ j | pij(n) - πj | < ε for all n ≥ τ(ε).
This is closely related to the magnitude of the second-largest eigenvalue of P, say λ2. The smaller is |λ2| then the smaller is the mixing time. In fact, one can prove bounds such as
|λ2| log(1/(2 ε))/(2(1−|λ2|)) ≤ τ(ε) ≤ log(1/(π* ε))/(1−|λ2|)
where π* is the smallest component of π (the invariant distribution).
Other quantities that are interesting are the coupling time (the time for two independent copies of the Markov chain to couple) and the cover time (the time for the Markov chain to visit every state at least once).
I concluded the lecture with a demonstation how Engel's probabilistic abacus can be used to calculate the invariant distribution of a finite-state Markov chain in which all p_{ij} are rational numbers. The puzzle is "why does this algorithm always terminate in a finite number of steps?" There is more about this algorithm in Example Sheet 2, #15 and Section 12.5 of the notes. I first heard about this problem from Laurie Snell circa 1975. At that time he said that the questions as why it works was still open.
Lecture 9
Today's lecture was a high point in our course: the proof by coupling that for an ergodic Markov chain P(X_n=i) tends to the equilibrium probability pi_i as n tends to infinity.
In response to a good question that a student asked during the lecture I have slightly modified in the notes the wording to the proof of Theorem 9.1, for the part (iii) implies (i).
I mentioned Vincent Doblin (1915-40) [also known as Wolfgang Doeblin] to whom is due the coupling proof of Theorem 9.8. There is a good article about his life in a 2001 article in The Telegraph: Revealed: the maths genius of the Maginot line. Some of Doblin's work was only discovered in summer 2000, having been sealed in an envelope for 60 years.
I quoted J. Michael Steele on coupling:
Coupling is one of the most powerful of the "genuinely probabilistic" techniques. Here by "genuinely probabilistic'' we mean something that works directly with random variables rather than with their analytical co-travelers (like distributions, densities, or characteristic functions.
I like the label "analytic co-travelers". The coupling proof should conv ince you that Probability is not merely a branch of Analysis. The above quote is taken from Mike's blog for his graduate course on Advanced Probability at Wharton (see here). Mike has a fascinating and very entertaining web site, that is full of "semi-random rants" and "favorite quotes" that are both funny and wise (such as his "advice to graduate students"). I highly recommend browsing his web site. It was by reading the blogs for his courses that I had the idea of trying something similar myself this year. So if you have been enjoying this course blog - that is partly due to him. Here is a picture of Mike and me with Thomas Bruss at the German Open Conference in Probability and Statistics 2010, in Leipzig.
The playing cards for the magic trick that I did in the lecture were "dealt" with the help of the playing card shuffler at random.org. By the way, there is a recent interview with Persi Diaconis in the October 27 (2011) issue of Nature, entitled "The Mathemagician".
The following is a little sidebar for those of you who like algebra and number theory.
In the proof of Lemma 9.5 we used the fact that if the greatest common divisor of n1,..., nk is 1 then for all sufficiently large n there exist some non-negative integers a1,..., ak such that
n = a1 n1 + ··· + ak nk. (*)
Proof. Think about the smallest positive integer d that can be expressed as d = b1 n1 + ··· + bk nk for some integers b1,..., bk (which may be negative as well as non-negative). Notice that the remainder of n1 divided by d is also of this form, since it is r =n1 − m (b1 n1 + ··· + bk nk) for m=⌊n1 /d⌋. If d does not divide n1 then r<d, and d fails to be the smallest integer that can be expressed in the form d = b1 n1 + ··· + bk nk. Thus we must conclude that d divides n1. The same must be true for every other nj, and so d=gcd(n1,...,nk)=1. So now we know that it is possible to write 1 = b1 n1 + ··· + bk nk, and so also we know we can write j = j (b1 n1 + ··· + bk nk), for all j=1,..., n1. Finally, we can leverage this fact to conclude that for some large N we can write all of N, N+1, N+2,..., N+n1 in the required form (*), and hence also we can also express in form (*) all integers N + m n1 + j, where m and j are non-negative integers, i.e. we can do this for all integers n≥ N. (This is a proof that I cooked up on the basis of my rather limited expertise in algebra. Perhaps one of you knows a quicker or more elegant way to prove this little fact? If so, please let me know.)
Lecture 8
Following the lecture I have made a correction to Theorem 8.4 (iii) which should be "0< γik < ∞ for all i". Earlier, I made a correction to Page 31, line 4. I have also added the words "under P_k" to the fourth line of the proof of Theorem 8.4. As I commented in lectures, the hypothesis that P is recurrent is used in this proof, since the proof relies on the fact that T_k < ∞. This comment is written at 2pm Tuesday - so re-download the notes if your copy is prior to then.
Notice that the final bits of the proofs of both Theorems 8.4 and 8.5 follow from Theorem 8.3. In Theorem 8.4, the fact of (iii) follows from Theorem 8.3 once we have proved (i) and (ii). And in Theorem 8.5 the fact that mu=0 follows from Theorem 8.3 because mu_k=0. However, in the notes the proofs of Theorems 8.4 and 8.5 are self-contained and repeat the arguments used in Theorem 8.3. (These proofs are taken directly from James Norris's book.)
In today's lecture we proved that if the Markov chain is irreducible and recurrent then an invariant measure exists and is unique (up to a constant multiple) and is essentially γk, where γik is the expected number of hits on i between successive hits on k. The existence of a unique positive left-hand (row) eigenvector is also guaranteed by Perron-Frebonius theory when P is irreducible (see the blog on Lecture 2). This again points up the fact that many results in the theory of Markov chains can be proved either by a probabilistic method or by a matrix-algebraic method.
If the state space is finite, then clearly sum_i γik < ∞, so there exists an invariant distribution. If the state space in infinite sum_i γik may be < ∞ or =∞, and these correspond to the cases of positive and null recurrence, which we will discuss further in Lecture 9.
We looked at a very simple model of Google PageRank. This is just one example of a type of algorithm that has become very important in today's web-based multi-agent systems. Microsoft, Yahoo, and others have proprietary algorithms for their search engines. Similarly, Amazon and E-bay run so-called recommender and reputation systems. Ranking, reputation, recommender, and trust systems are all concerned with aggregating agents' reviews of one another, and of external events, into valuable information. Markov chain models can help in designing these systems and to make forecasts of how well they should work.
Lecture 7
I played to you some Markov music, taken from the web site: Mathematics, Poetry, and Music by Carlos Pasquali. The tune is very monotonous and simple sounding because the distribution of nth note depends only on the (n−1)th note. More interesting music could be obtained by lettting the state be the last k notes, k>1. You might enjoy reading the Wikipedia article on Markov chains. It has a nice section about various applications of Markov chains to: physics, chemistry, testing, Information sciences, queueing theory, the Internet, statistics, economics and finance, social sciences, mathematical biology, games, music, baseball and text generation.
There are lots of other crazy things that people have done with Markov chains. For example, at the Garkov web site the author attempts to use a Markov chain to re-create Garfield comic strips. A much more practical use of Markov chains is in the important area of speech recognition. So-called hidden Markov models are used to help accurately turn speech into text, essentially by comparing the sound that is heard at time t with the possibilities that are most likely, given the sound heard at time t−1 and the modelling assumption that some underlying Markov chain is creating the sounds.
Today's lecture was an introduction to the ideas of an invariant measure and invariant distribution. I mentioned that the invariant distribution is also called a stationary distribution, equilibrium distribution, or steady-state distribution.
Several times today I referred to cards and card-shuffing (which have facinated me from childhood, and in my undergraduate days when I was secretary of the Pentacle Club). It is always good to have a few standard models in your mathematical locker (such as card-shuffling, birth-death chains, random walk on Z and Z^2, etc) with which you can test your intuition and make good guesses about what might or might not be true. The state space of a deck of cards is of size 52! (= 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277,824,000,000,000,000) (all the possible orders). Clearly, the equlibrium distribution is one in which each state has equal probability pi_i = 1/52!. I mentioned today that m_i=1/pi_i (which is intuitively obvious, and we prove rigorously in Lecture 9). This means that if you start with a new deck of cards, freshly unwrapped, and then shuffle once every 5 seconds (night and day), it will take you 1.237 x 10^{61} years (on average) before the deck returns to its starting condition. Notice that this result holds for any sensible meaning of a shuffle, provided that it has the effect of turning the state space into one closed class (an irreducible chain).
A very important question in many applications of Markov chains is "how long does it take to reach equilbrium?" (i.e. how large need be n so that the distribution of X_n is almost totally independent of X_0?) You might enjoy reading about the work of mathematician/magician Persi Diaconis in answering the question "how many shuffles does it take to randomize a deck of cards?".
Lecture 6
There is now a comments thread at the end of the course page, where you may make comments, or ask questions. if you subscribe then you will be sent an email whenever I annouce in the comments that the course notes have been updated.
This lecture marks the half way point of the course. We celebrated by proving George Polya's famous theorem (1921): that symmetric random walk is recurrent on Z and Z^2, but transient on Z^d (d>2). In fact, we only proved transience only for d=3, but it is easy to see that this implies transience for all d>2 (Example Sheet 2, #2).
I mentioned and recommended Polya's famous little book "How to Solve It". I also quoted this story (from A. Motter):
While in Switzerland Polya loved to take afternoon walks in the local garden. One day he met a young couple also walking and chose another path. He continued to do this yet he met the same couple six more times as he strolled in the garden. He mentioned to his wife: how could it be possible to meet them so many times when he randomly chose different paths through the garden?
I talked a bit about electrical networks in which each edge of an infinite graph is replaced with a 1 ohm resistor. I am thinking here not only of graphs such as the regular rectangular or honeycomb lattice, but also graphs as strange as the Penrose tiling (which gives us a non-periodic graph). I told you that the resistence between two nodes in such a network tends to infinity (as the nodes are chosen a distance from one another that tends to infinity) if and only if a symmetric random walk on the same graph is recurrent. I will say more about why this is so in Lecture in 12.
Meanwhile, you can apply today's lecture to Example Sheet 1 #15. It is pretty easy to see from the hint that if we know that symmetric random walk on Z^2 is recurrent then symmetric random walk on a honeycomb lattice must also be recurrent. But proving the converse is harder! In fact, one can show that random walk on every sort of sensibly-drawn planar graph is recurrent. To prove this we must decide what we mean by a "sensibly-drawn planar graph" and then find a way to embed any such graph in in some other graph on which we know random walk is recurrent. You can learn more about the details of this in Peter Doyle and Laurie Snell's Random walks and electric networks, 2006 (freely available to download).
The material in Section 6.5 (Feasibility of wind instruments) was written after a short email correspondence with Peter Doyle. The story about cities which beggar their neighbours is my own fanciful invention, but it makes that same point without needing to brush up on the theory of fluid dynamics..
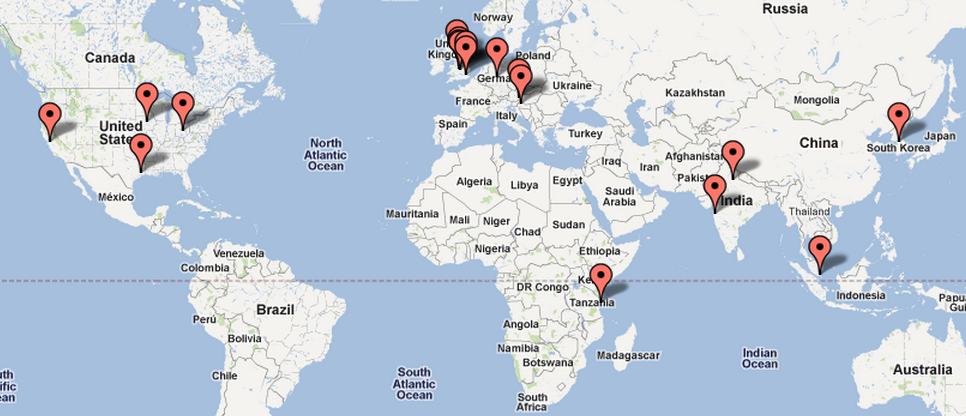
This map shows the sources of visitors to this Markov Chains course web site over the past 4 days (20-23 October). Visitors to the course page are averaging about 45 per day and on this blog page about 15 per day. It seems that about 25% of the hits to the course page are from outside Cambridge.
Lecture 5
Today's lecture was on recurrence and transience. First let me clear up a two points that arise from some students' questions.
1. We make the definition that state i is recurrent if P_i(V_i = ∞)=1. It is defined to be transient otherwise, i.e if P_i(V_i = ∞)<1. Later (in Theorem 5.3) we show that if i is transient then actually P_i(V_i = ∞)=0 (but this is a consequence, not part of our starting definition of transience).
2. In the proof of Theorem 5.4 we use the fact that p_{ii}^(n+m+r) ≥ p_{ij}^(n) p_{jj}^(r) p_{ji}^(m). Please don't think that we are using any summation notation! (We never use summation convention in this course.) This inequality is a simply product of three terms on the right hand side and is a simple consequence of the fact that one way to go i→i in n+m+r steps is to first take n steps to go i→j, then r steps to go j→j, and finally m steps to go j→i. There is a ≥ because there are other ways to go i→i in n+m+r steps.
In Theorem 5..5 we gave an important way to check if a state is recurrent or transient, in terms of the summability of the p_{ii}^(n). This criterion will be used in Lecture 6. There are other ways to check for transience. One other way is to solve the RHE for the minimal solution to
y_j = sum_k p_{jk} y_k, j neq i, and
y_i=1.
So y_j =P_j(return to i). Now check the value of sum_k p_{ik} y_k. If it is <1 then i is transient. This is essentially the content of Theorem 5.9, which I have put in my published notes but am not going to discuss in lectures. However, you may find it helpful to read the Theorem. It's proof is simple.
I talked for a few minutes about my research on on-line bin packing, in the paper Markov chains, computer proofs, and average-case analysis of best fit bin packing. In this research we consider items, of sizes which are uniformly chosen amongst the intergers 1,2,...,8, say, that arrive in a stream, and as each item arrives it must be packed in a bin. Initially there are an infinite number of empty bins, of some size, say 11. In the Markov chain that models the process of on-line best-fit bin packing the state can be represented as (x1,x2,..,x10), where xi is the number of bins that we have started, but which are not yet full, and which have a gap of i. It is interesting to ask if infinitely there is a return to the state (0,0,...,0) in which there are no partially-full bins present (i.e. if the Markov chain is recurrent). You might like to view these seminar sildes for more details. (These were for a faculty colloquium and aimed at a general audience of mathematicians, and so it should be well within your knowledge of mathematics to understand these slides.)
In the on-line bin packing research (and many other problems in queueing theory) researchers often prove results about recurrence and transience using some more sophisticated ideas than in Theorems 5.4. and 5.9 of today's lecture. One of these ideas is Foster's criterion. This says that an irreducible Markov chain is recurrent if we can find a function f : I → R (called a Lyapounov function) and a finite subset of the state space, say J, such that (a) E[ f(X_1) | X_0=i ] ≤ f(i) for all i not in J, and (b) for each M>0 the set of states for which f(i)≤M is finite. Part (a) is essentially saying that outside J there is always drift back to states where f is smaller.
Lecture 4
In today's lecture we had the definition of a stopping time. This brings to my mind a small riddle (which I think I heard from David Kendall). "How do you make perfect toast? Answer: Wait until it smokes – then 10 seconds less."
Stopping times play a large role in probability theory. One very important idea is the following. Consider Example Sheet 1 # 10, the gambler's ruin problem played on {0,1,...,10} in the fair game case (p=q=1/2). If the gambler has i and bets j (1≤j≤i), she is equally likely to next have i−j or i+j. So E(X_{n+1} | X_n)=X_n, no matter how much she bets. This implies that E(X_{n+1} | X_0)=X_0 no matter how she bets. It is a theorem (Doob's optional sampling theorem) that E(X_T | X_0)=X_0 for any stopping time T (such that ET< infinity, as indeed must be the case for any stopping time in this problem). Thus, we see that there is no way that the gambler can make any expected profit (or loss), no matter how clever a strategy she uses in choosing the sizes of her bets and when to stop gambling.
The optimal sampling theorem also gives us a quick way to answer the first part of Example Sheet 1 #10. If T is the first time that X_n hits either 0 or 10, then E(X_T | X_0=2)=2 implies P_2(hit 0)0+P_2(hit 10)10 = 2. Hence P_2(hit 10)=1−P_2(hit 0)=1/5. That's even easier than solving the RHEs!
In lectures today I forget to make the comment that the interchange of E_i and sum_{j in I} that occurs halfway down page 14 is an application of Fubini's theorem. This theorem says that we can reverse the order of sums, i.e.
sum_i sum_j a_{ij} i = sum_j sum_i a_{ij}
when these are sums over countable sets and the sum is absolutely convergent. Fubini's theorem is presented in more generality in Part II Probability and Measure.
Section 4.1 is of course a general version of Example Sheet 1 #12. When doing #12, make sure you understand how the condition of "minimal non-negative solution" is being used.
I spent the final 10 minutes of this lecture describing Arthur Engel's probabilistic abacus (a chip firing game) for calculating absorption probabilities in a finite-state Markov chain in which all entries of P are rational. My slides and commentary are in Appendix C, and also an exposition of Peter Doyle's proof that the algorithm really works. I first heard about this abacus in 1976 when Laurie Snell was visiting the Statistical Laboratory. Snell (1925-2011) was a student of Joe Doob, one of the 'greats' of probability theory, whose optional sampling theorem I have mentioned above. Snell is the author (with John Kemeny) of several classic textbooks (including one called "Finite Markov Chains"). He is founder of Chance News (which can be fun to browse). A particular memory that I have of Professor Snell is that he liked to go to London to play roulette at the casinos there. This struck me that is a very peculiar recreation for an expert in probability. But I think it was for fun - he never claimed to make money this way.
You might be amused to know that Question #10 on Example Sheet 1 is a actually an old tripos question from 1972, (Paper IV, 10C). I took IB in 1973 so you and I share at least one question upon which we have practiced as students.
Until now there were several typos in the published notes for Lecture 4. Please make sure you have a current copy, which I think is now fully accurate.
Lecture 2 (more)
The fact that we can solve for p_11^{(n)} in the stated form follows from the fact that p_{11}^{(n)} satisfies recurrence relations given by
q(P)_{11} = 0
where q(x)=det(xI−P) is the characteristic polynomial. By the Caley-Hamilton theorem we know q(P)=0 (see IB Linear Algebra)). You know how to solve such recurrence relations (from IA Differential Equations). I have already said something about this is my earlier blog entry for Lecture 2. In particular, although some matrices cannot be diagonalized, every square matrix P can be written in Jordan normal form, P=UJU^{−1} (see IB Linear Algebra), and P^n=UJ^nU^{−1} is then of the form that takes account of repeated eigenvalues.
I believe that a good mathematician these days should not only understand theory and proofs, but also be able to use modern computing tools to quickly work out examples.
I highly recommend that you install Mathematica and use it while you study and work on examples sheets (in many courses). I personally use it on almost a daily basis. You can download a free copy:
http://www.damtp.cam.ac.uk/internal/computing/software/mathematica/
It is very easy install and learn to use. The time you spend learning to use it (and similarly MATLAB) is a very good investment.
Below is a short Mathematica program that does Example Sheet 1, #7. I think that a well-motivated student might like do this question by hand, and then subsequently check the answer using Mathematica. By the way, I would not expect an examiner to set a question in tripos that is as difficult to do by hand as doing all of (a) (b) and (c) in #7. However, it would be fair to ask the answer for just one value of p.
Clear[P,p,p11]
P={{0,1,0},{0,2/3,1/3},{p,1−p,0}};
(* Solution to (a) *)
mu=Eigenvalues[P /. p→1/16]
p11[n_]=a mu[[1]]^n+ b mu[[2]]^n+ c mu[[3]]^n;
Solve[{p11[0]==1,p11[1]==0,p11[2]==0},{a,b,c}]
p11[n] /. %[[1]] //Expand
Out[1]= {1,-(1/4),-(1/12)}
Out[2]= {{a->1/65,b->-(2/5),c->18/13}}
Out[3]= 1/65-1/5 (-1)^n 2^(1-2 n)+1/13 (-1)^n 2^(1-2 n) 3^(2-n)
(* Solution to (b) *)
mu=Eigenvalues[P /. p->1/6]
p11[n_]=a mu[[1]]^n+ b mu[[2]]^n+ c mu[[3]]^n;
Solve[{p11[0]==1,p11[1]==0,p11[2]==0},{a,b,c}]
p11[n] /. %[[1]] //ComplexExpand
Out[4]= {1,-(1/6)+I/6,-(1/6)-I/6}
Out[5]= {{a->1/25,b->12/25-(9 I)/25,c->12/25+(9 I)/25}}
Out[6]= 1/25+1/25 2^(3-n/2) 3^(1-n) Cos[(3 n \[Pi])/4]+1/25 2^(1-n/2) 3^(2-n) Sin[(3 n
\[Pi])/4]
(* Solution to (c) *)
mu=Eigenvalues[P /. p->1/12]
p11[n_]=a +(b+c n)mu[[2]]^n;
Solve[{p11[0]==1,p11[1]==0,p11[2]==0},{a,b,c}]
p11[n] /. %[[1]]
Out[7]= {1,-(1/6),-(1/6)}
Out[8]= {{a->1/49,b->48/49,c->-(6/7)}}
Out[9]= 1/49+(-(1/6))^n (48/49-(6 n)/7)
Lecture 3
You should now be able to do all of Example Sheet 1 (excepting that #12 will be easier after seeing Section 4.1 in the next lecture).
I mentioned that Theorem 3.4 in this lecture is similar to the result that you were taught in Probability IA, concerning the probability of ultimate extinction of a branching process. Remember that in a branching process each individual independently produces offspring for the next generation, according to a distribution in which there are k offspring with probability p_k (k=0,1,...). Given that we start with one individual, the probability of ultimate extinction, say u, is the minimal solution to
u = G(u) = sum_k p_k uk
where G is the probability generating function for the number of offspring.
Do you remember the proof that u is the minimal solution to u=G(u) , and do you see how similar it is to the proof in Theorem 3.4?
I have called the equations of the form x=Px (i.e. x_i = sum_j p_{ij}x_j) "right-hand equations", because x appears on the right-hand side of P. Later in the course we will find a use for "left-hand equations", of the form x=xP. So far as I can tell, this terminology does not appear in any modern books on Markov chains. However, it was language used by David Kendall in the course I took from him in 1972 and I have always found it to be helpful terminology.
I hope you enjoy question #13 on Example Sheet 1 (which is a new question this year). It contains a result that many people find surprising. In a Red-Black game in which p<q the strategy of bold play is optimal (but not necessarily uniquely so). This fact is proved in the Part II course Optimization and Control (see Section 4.3 "Optimal gambling" in the Optimization and Control course notes.) Part of that course is about Markov Decision Processes, which are Markov chains in which we have some control over the transitions that occur, and we try to minimize (or maximize) costs (or rewards) that accrue as we move through states.
Question #14 on the examples sheet extends the idea of a gambling game between 2 players to that of a game amongst 3 players. It is remarkable that there is such a nice formula for the expected number of games until one of the first player becomes bankrupt.
Lecture 2
Following this lecture you should be able to do Example Sheet 1, #1−9 (except 8 (b), although you can probably guess what is meant).
Someone has rightly pointed out that at the bottom of page 2 of the notes, the line should end p_{ i_{i−1} i_n }. This has now been corrected into the notes.
Following the lecture someone asked me a question about the eigenvectors of matrices, specifically, "Is the set of eigenvalues obtained from left-hand eigenvectors the same as that obtained from right-hand eigenvectors?" (The answer is yes.) This question tells me that I might have referred to facts of linear algebra that are fairly new to you, or only briefly covered in the IA Vectors and Matrices course. In the IB Linear Algebra course you will learn more. For example, the schedules include "Algebraic and geometric multiplicity of eigenvalues. Statement and illustration of Jordan normal form." It will be interesting for you to think again about calculation of P^n once you know that it is always possible to write P=UJU^{−1}, where J is an almost diagonal matrix and U is a matrix whose rows are left-hand eigenvectors. Having said this, we shall not actually need any advanced results from linear algebra in our course. Most of our proofs are probabilistic rather than matrix-algebraic. Today's discussion of P^n is perhaps the one exception, since if you wish to fully understand the solution of the recurrence relations when the characteristic polynomial has repeated roots then the representation P=UJU^{−1} is helpful.
This lecture was mostly about how to calculate the elements of P^n by solving recurence relations. We ended the lecture with definitions of "i communicates with j", the idea of class, and closed and open classes. If the Markov chain consists of only one class (and so every state can be reached from every other) then the Markov chain is said to be irreducible.
Notice that if P is m x m and irreducible then Q=(1/m)(I+P+P^2+···+P^{m-1}) is a transition matrix all of whose elements are positive (can you see why? A hint is the pigeonhole principle).
Here now is a sidebar on some interesting results in matrix algebra that are related to today's topics. We said in this lecture that if P is m x m and has m distinct eigenvalues, 1, mu_2, ..., mu_m, then
p_{ij}^{(n)} = a_1 + a_2 mu_2^n + ··· + mu_m^n
for some constants a_1, a_2, ..., a_m.
We would like to know more about the eigenvalues mu_2, ...., mu_m. In particular, let |mu_j| denotes the modulus of mu_j. If |mu_j|<1 for all j>1 then p_{ij}^{(n)} tends to a_1 as n tends to infinity (as we see happening in Example 2.1)
We claim the following.
- |mu_j| ≤ 1 for all j>1.
- Suppose there exists n such that P^n is strictly positive. Then |mu_j|<1 for all j>1, and so p_{ij}^{(n)} tends to a_1 as n tends to infinity.
These facts are consequences of Perron-Frebonius theory. This theory (dating from about 100 years ago and useful in many branches of mathematics) says the following.
Suppose A is square matrix, which is non-negative and irreducible (in the sense that for all i,j , we have (A^n)_{ij}>0 for some n). Then there exists a positive real number, say lambda, such that (i) lambda is an eigenvalue of A, (ii) lambda has multiplicity 1, (iii) both the left and right-hand eigenvectors corresponding to lambda are strictly positive, (iv) no other eigenvector of A is strictly positive, (v) all eigenvalues of A are in modulus no greater than lambda, (vi) if, moreover, A is strictly positive then all other eigenvalues of A are in modulus strictly less than lambda, and
(vii): min_i sum_j a_{ij} ≤ lambda≤ max_i sum_j a_{ij}.
i.e. lambda lies between the minimum and maximum of row sums of A.
So in the case that A =P (i.e. the transition matrix of an irreducible Markov chain), (vii) implies that lambda=1 (and (1,1,...,1) is the corresponding right-hand eigenvector).
Of the claims made earlier, 1 follows from (v) and (vii). To see 2, we have from (vi) that if P^n is strictly positive then all its eigenvalues different to 1 are in modulus less strictly than 1. But if mu is an eigenvalue of P then mu^n is an eigenvalue of P^n. Hence we must have |mu|<1.
As mentioned above, if P is irreducible then Q=(1/m)(I+P+P^2+···+P^{m−1}) must be positive (i.e. a matrix of positive elements). Thus from Perron-Frebonius theory, Q has a largest eigenvalue 1 and all its other eigenvalues are strictly less than 1. From these observations it follows that
Q^n tends to a limit as n tends to infinity.
Notice that a Markov chain with transition matrix Q can be obtained by inspecting our original chain at times 0, 0+Y_1, 0+Y_1+Y_2, 0+Y_1+Y_2+Y_3, ..., where the Y_i are i.i.d. random variables, each being uniformly distributed over the numbers 0,1,...,m−1.
Lecture 1
Lecture 1 was on Thursday October 6 at 10am. It was attended by almost all IB students. Some notes are already on line. Something fun is Appendix C.
The
introduction of a jumping frog (who I called Fred) into Example 1.1 is window-dressing.
However, the frog and lily pad metaphor was used by Ronald A. Howard in
his classic book Dynamic Programming and Markov Processes
(1960). I read this book long ago and the image has stuck
and been helpful. It gets you thinking in pictures, which is good.
Markov
chains are a type of mathematics that I find to be highly visual,
by which I mean that the problems, and even the proofs (I'll give
examples later), can be run through my mind (and yours) in a very
graphic way - almost like watching a movie play out.
Our course only deals with Markov chains in which the state space is countable. Also, we focus on a discrete-time process, X_0, X_1, X_2, ... , It is really not fundamentally different to deal with Markov processes that have an uncountable state space (like the non-negative real numbers) and which move in continuous time. The mathematics becomes only mildly more tricky. An important and very interesting continuous-time Markov process is Brownian motion. This is a process (X_t)_{t ≥ 0} which is continuous and generalizes the idea of random walk. It is very useful in financial mathematics.
Someone asked me afterwards to say more about simulation of a Markov chain. I am talking about simulation of a Markov chain using a computer. Think about how we might simulate the outcome of tossing a fair coin on a computer. What we do it ask the computer to provide a sample of a uniform random variable on [0,1]. In Mathematica, for example, this could be done with the function call U=Random[ ]. If U<1/2 we say Tails, and if U≥1/2 we say Heads.
Similarly, if we wished to simulate the two-state Markov chain in Example 1.4 we would, if X_n=1, set X_{n+1}=1 if U lies in the interval [0,1−alpha) and set X_{n+1}=2 if U lies in [1−alpha,1]. If X_n=2, we would set X_{n+1}=1 if U lies in [0,beta) and set X_{n+1}=2 if U lies in [beta,1]. The content of Section 1.4 generalizes this idea in an obvious way. Simulation of random processes via a computer is an important tool. For example, we might like to run a computer simulation of road traffic network to see what delays occur when we try different strategies for sequencing the traffic lights at intersections.
Section 1.6 is about the calculation of P^n when P is a 2x2 matrix. We found P^n by writing P=UDU^{−1}, where D=DiagonalMatrix[{1,1−alpha−beta}]. We did not need to know U explicitly. But, as an exercise, we can easily find it. Notice that for any stochastic matrix P there is always a right-hand eigenvector of (1,1,....,1) (a column vector), since row sums of P are 1. So there is always an eigenvalue of 1. The other right-hand eigenvector is (alpha,−beta), with eigenvalue of 1−alpha−beta. So we could take U^{−1}={{1,alpha},{1,−beta}}. Can you also find the left-hand eigenvectors? They are of course the rows of U.
In Section 1.6 I gave two methods of finding p_{11}^{(n)}. The first method obviously generalizes to larger matrices. The second method is specific to this 2x2 example, but it is attractive because it gets to the answer so quickly.
Notice that throughout my blog I use pseudo-LaTeX notation for mathematics. So x_i is "x sub i", alpha is the Greek character alpha, and so forth. (I say pseudo-LaTeX, because in actual-LaTeX one has to put $ signs around things, e.g. $x_i$, and put a \ in front of a Greek character name, e.g. \alpha). LaTeX is the language in which my lecture notes (and almost all modern mathematical papers) are written. When I want to do some algebra or work with mathematical objects I sometimes use Mathematica's notation. So DiagonalMatrix[{1,1−alpha−beta}] is the 2x2 diagonal matrix which has 1 and 1−alpha−beta on the diagonal. Also, {{1,alpha},{1,−beta}} is the 2x2 matrix whose rows are {1,alpha} and {1,−beta}.
There was one typo in the notes that were on this site until today. You should note this if you downloaded a copy of the notes before today. In Theorem 1.3 the statement should be "if and only if" not just "if". As I said, this theorem is not particularly deep, but it gives us practice in using the notation and understanding how Markov chains work.
You will need the ideas in Section 1.2 to do Example Sheet 1 #2, #3 and #4.
12.45pm on Thursday 6/10/11
Please send me email with comments or corrections on my lectures, the notes or the example sheets. I am very glad to receive comments and suggestions from students studyng the course.
This material is provided for students, supervisors (and others) to freely use in connection with this course. Copyright remains with the author.
University of Cambridge > Mathematics > Statistical Laboratory > Richard Weber > Markov Chains > Course Blog
Number of visits to this page since 20/10/11:
Richard Weber ( rrw1@cam.ac.uk ) Last modified: November 2011