Course information
This is a home page of information for Richard Weber's course of 12 lectures to second year Cambridge mathematics students in autumn 2012. This material is provided for students, supervisors (and others) to freely use in connection with this course. A web page for the 2011 course home page is also still available.
-
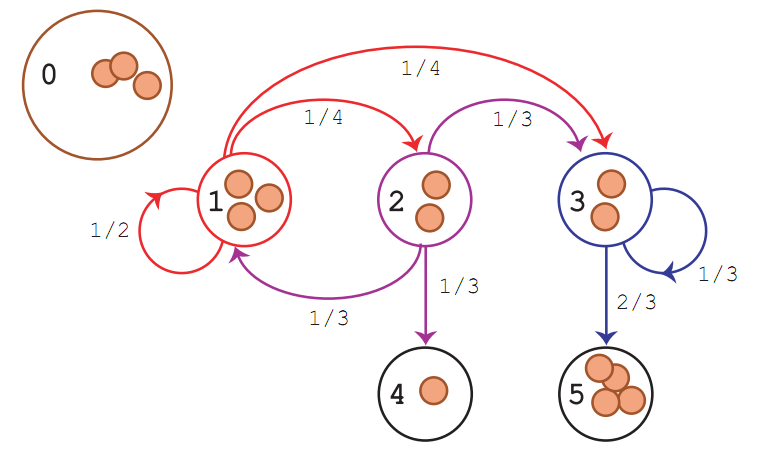
Engel's probabilistic abacus
(a chip firing game for calculating absorption probabilities - see Appendix C)
Course notes
The course closely follows Chapter 1 of James Norris's book, Markov Chains, 1998 (Chapter 1, Discrete Markov Chains is freely available to download and I recommend that you read it.) I am also publishing some notes. Each lecture has notes of 3.5–4 pages.
These notes are now complete (subject to any small typos that may still be found). They include:
- Table of Contents
- Schedules and learning outcomes
- Lectures 1 – 12
- Appendix A. Probability spaces
- Appendix B. Historical notes
- Appendix C. The probabilistic abacus for absorbing Markov chains
- Index
The notes have hyperlinks. If you click on an entry in the table of contents, or on a page number in the Index, you be taken to the appropriate page.
If you think you find a mistake in these notes, check that you have the most recent copy (as I may have already made a correction.) Otherwise, please let me know and I will incorporate that correction into the notes.
Here also are the overhead slides that I sometimes used in lectures.
Course Blog
There is a course blog in which I am writing a few comments after each lecture: to emphasize an idea, give a sidebar, correction (!), or answer an interesting question (that perhaps a student sends to me in email).
Comments, Discussion and Questions
This year I am organising these pages so that students can comment or ask questions on the discussion page, and also at the end of each of the blog posts. I expect some good contributions. I will endeavour to answer questions. When you comment, you can do this anonymously if you wish. Just give any name and leave the email address box blank.
You can also send me email with questions, suggestions or if you think you have discovered a mistake in the notes.
Examples sheets
There are 2 examples sheets, each containing 13 questions, as well as 3 or 4 "extra" optional questions. The extra questions are interesting and off the well-beaten path of questions that are typical for an introductory Markov Chains course. You should receive a supervision on each examples sheet.
- Example sheet 1 (for Lectures 1 – 5)
- Example sheet 2 (for Lectures 6 – 11)
Feedback
This year's course will finish on Tuesday 13 November 2012. The written feedback questionnaire has been completed by __ students, and a further __ have completed the electronic form. If you have not yet given feedback you can do so using my equivalent on-line form. This will be sent to my email anonymously. After reading the responses, I will forward them to the Faculty Office.
Past exam questions
Here is single fille of all the tripos examination questions on Markov Chains from 2001 to last June. Questions prior to 2004 are from a former Part II course, so I have crossed out those that are not relevant to the present IB course.
Recommended books
- G.R. Grimmett and D.R. Stirzaker Probability and Random Processes. OUP 2001 (Chapter 6.1-6.5 is on discrete Markov chains.)
- J.R. Norris Markov Chains. CUP 1997 (Chapter 1, Discrete Markov Chains is freely available to download. I highly recommend that you read this chapter. If you need to brush up of your knowledge of how to solve linear recurrence relations, see Section 1.11.)
Other resources and further reading
Sheldon Ross, Introduction to Probability Models, 2006 (Chapter 4) and Stochastic Processes,1995 (Chapter 4) (Each of these books contains a readable chapter on Markov chains and many nice examples. The author does a good job of making difficult concepts seem fairly simple.) See also, Sheldon Ross and Erol Pekoz, A Second Course in Probability, 2007 (Chapter 5 gives a readable treatment of Markov chains and covers many of the topics in our course. In other chapters this book provides a gentle introduction to probability and measure theory.)
Charles Grinstead and Laurie Snell Introduction to Probability Second edition, 1997 (freely available to download). This book is also quite easy to read. The authors have good insight and you will find some gems here. Chapter 11 is on Markov Chains. This book it is particulary interesting about absorbing chains and mean passage times. There are many nice exercises, some notes on the history of probability, and on pages 464-466 there is information about A. A. Markov and the early development of the field. There are two distinct approaches to the study of Markov chains. One emphasises probabilistic methods (as does Norris's book and our course); another is more matrix-based, as it this book. The probabilistic methods are more satisfying, but it is good to know something about the matrix methods too.)
Takis Konstantopoulos has a nice set of course notes on Markov Chains and Random Walks, 2009, at a somewhat more in-depth level than our course. You might like to browse through his notes.
David Aldous and Jim Fill Reversible Markov Chains and Random Walks on Graphs, 1994-2001 (This monograph is freely available and a great souce of delightful information and insightful comment. It covers much more advanced topics that in our course. However, Chapters 1-3 are well within your grasp, and to read them will deepen your understanding.)
Peter Doyle and Laurie Snell Random walks and electric networks, 2006 (freely available to download. You could read this (easy to understand) paper to learn more about the interesting connection between recurrence/transience properties of random walks and resistence in electrical network, as I will briefly discuss in Lecture 12.
David Levin, Yuval Peres and Elizabeth Wilmer Markov Chains and Mixing Times, 2008. Chapters 1 and 2 nicely summarise most of the content of our course in a small number of pages. However, I reference this textbook mainly because it is a good place to read about some of the fascinating topics within the field of Markov chains that interest researchers today. For example, Chapter 5 on Coupling, will tell you how the ideas we used in Lecture 9 can be extended. This is a book you wiill want to read if ever go beyond undergraduate study in this field.
The PageRank citation ranking: bringing order to the web (by Lawrence Page, Sergey Brin, Rajeev Motwani, and Terry Winograd, 1998) describes the workings of the Google PageRank algorithm and the part that Markov chains play in this. This is discussed in brief in Lecture 8, Example 8.6 (random surfer). See also the Wikipedia article about PageRank.
Peter Winkler, Mathematical Mind Benders, 2007. This is not a book on Markov Chains, but a collection of mathematical puzzles that I recommend. Many of the puzzles are based in probability. It includes the "Evening out the Gumdrops" puzzle that I discuss in lectures, and lots of other great problems. He has an earlier book also, Mathematical Puzzles: a Connoisseur's Collection, 2003.
Frederick Mosteller, 50 Challenging Problems in Probability, with Solutions, 1987. This is a classic book which anyone who is interested in probability should enjoy.
David Aldous has an interesting page of his reviews of many non-technical books related to probability. You might enjoy thinking about the points made in his posting:Presenting probability via math puzzles is harmful.
Schedules
Definition and basic properties, the transition matrix. Calculation of n-step transition probabilities. Communicating classes, closed classes, absorption, irreducibility. Calculation of hitting probabilities and mean hitting times; survival probability for birth and death chains. Stopping times and statement of the strong Markov property. [5]
Recurrence and transience; equivalence of transience and summability of n-step transition probabilities; equivalence of recurrence and certainty of return. Recurrence as a class property, relation with closed classes. Simple random walks in dimensions one, two and three. [3]
Invariant distributions, statement of existence and uniqueness up to constant multiples. Mean return time, positive recurrence; equivalence of positive recurrence and the existence of an invariant distribution. Convergence to equilibrium for irreducible, positive recurrent, aperiodic chains *and proof by coupling*. Long-run proportion of time spent in given state. [3]
Time reversal, detailed balance, reversibility; random walk on a graph. [1]
Contents
1 Definitions, basic properties, the transition matrix1.1 An example and some interesting questions1.2 Definitions1.3 Where do Markov chains come from?1.4 How can we simulate them?1.5 The n-step transition matrix1.6 P^{(n)} for a two-state Markov chain
2 Calculation of n-step transition probabilities, class structure, absorption, and irreducibility2.1 Example: a three-state Markov chain2.2 Example: use of symmetry2.3 Markov property2.4 Class structure2.5 Closed classes2.6 Irreducibility
3 Hitting probabilities and mean hitting times3.1 Absorption probabilities and mean hitting times3.2 Calculation of hitting probabilities and mean hitting times3.3 Absorption probabilities are minimal solutions to RHEs3.4 Gambler's ruin
4 Survival probability for birth and death chains, stopping times4.1 Survival probability for birth death chains4.2 Mean hitting times are minimal solutions to RHEs4.3 Stopping times4.4 Strong Markov property
5 Recurrence and transience5.1 Recurrence and transience5.2 Equivalence of recurrence and certainty of return5.3 Equivalence of transience and summability of n-step transition probabilities5.4 Recurrence as a class property5.5 Relation with closed classes
6 Random walks in dimensions one, two and three6.1 Simple random walk on Z6.2 Simple symmetric random walk on Z^26.3 Simple symmetric random walk on Z^36.4 *A continuized analysis of random walk on Z^3*6.5 *Feasibility of wind instruments*
7 Invariant distributions7.1 Examples of invariant distributions7.2 Notation7.3 What does an invariant measure or distribution tell us?7.4 Invariant distribution is the solution to LHEs7.5 Stationary distributions7.6 Equilibrium distributions
8 Existence and uniqueness of invariant distribution, mean return time, positive and null recurrence8.1 Existence and uniqueness up to constant multiples8.2 Mean return time, positive and null recurrence8.3 Random surfer
9 Convergence to equilibrium for ergodic chains9.1 Equivalence of positive recurrence and the existence of an invariant distribution9.2 Aperiodic chains9.3 Convergence to equilibrium *and proof by coupling*
10 Long-run proportion of time spent in given state10.1 Ergodic theorem10.2 *Kemeny's constant and the random target lemma*
11 Time reversal, detailed balance, reversibility, random walk on a graph11.1 Time reversal11.2 Detailed balance11.3 Reversibility11.4 Random walk on a graph
12 Concluding problems and recommendations for further study12.1 Reversibility and Ehrenfest's urn model12.2 Reversibility and the M/M/1 queue12.3 *The probabilistic abacus*12.4 *Random walks and electrical networks*12.5 Probability courses in Part II