University of Cambridge > Mathematics > Statistical Laboratory > Richard Weber > Optimization and Control

 This material is provided for students, supervisors (and others) to freely use in connection with this course. Copyright remains with the author.

Optimization and Control

picture of broom balancing Broom balancing as a control problem

This is home page for the course of 16 lectures taught to final year Cambridge mathematics students.

Introduction

The course builds a bit on Optimization IB, but there are really no prerequisites. Importantly we now add dynamic and stochastic elements that were not present in that course, and consider what happens when some variables are imperfectly observed. Applications of this course are to be found in science, economics and engineering (e.g., "insects as optimizers", "planning for retirement", "finding a parking space", "optimal gambling" and "steering a space craft to the moon"). The course should appeal to those who liked the type of problems occurring in Optimization IB, Markov Chains and Probability.

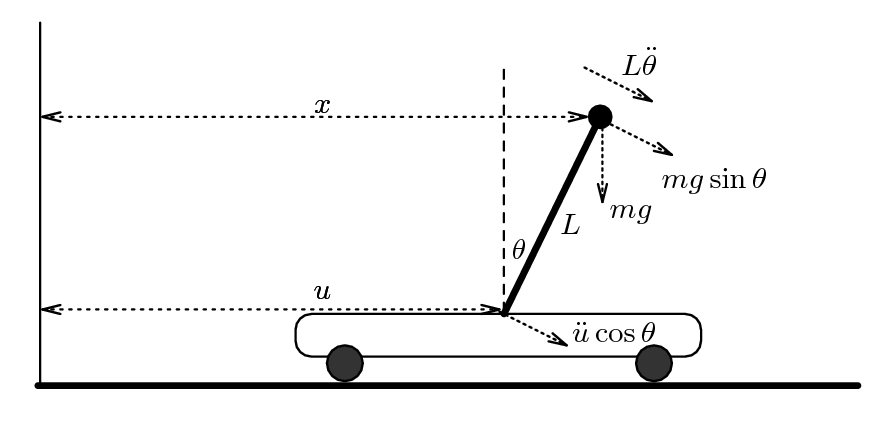
The diagram of the trolley on wheels at the top of this page models the problem that a juggler has when she tries to balance a broom upright in one hand. In this course you will learn how to balance N brooms simultaneously on top of one another, or perhaps side by side. Can you guess which of these two juggling trick is more difficult?

What's on this site

Each lecture is as self-contained as possible and has course notes amounting to four A4 pages. Click here for the table of contents and for schedules.

There are 3 examples sheets, with solutions, each containing about 12 questions. You should receive a supervision on each examples sheet. There is a file of past exam questions. There are four recommended books.

Please send me email with comments or corrections on my lectures, the notes or the examples sheet. I am very glad to receive comments and suggestions from students studyng the course.

This material is provided for students, supervisors (and others) to freely use in connection with this course. Copyright remains with the author. Notice to external persons accessing this page

Course notes

There are 74 pages of notes [contents (4), notes (68), index (2)].

The notes are in postscript and in Adobe Acrobat format (pdf files). Most computers have an Acrobat viewer installed, and if yours does not, one can be obtained for free. Acrobat provides for printing and display on a wide variety of devices. When you click below, you should begin to view the file on your screen with Acrobat. You can then mark and print the specific page or pages you require, rather than waste paper by printing all the pages.

La4.pdf - a single file of all lectures in A4 format

La5.pdf - a single file of all lectures in side-by-side A5 format

Individual lectures in side-by-side A5 format:

Table of Contents
L01 Dynamic Programming: The Optimality Equation
L02 Some Examples of Dynamic Programming
L03 Dynamic Programming over the Infinite Horizon
L04 Positive Programming
L05 Negative Programming
L06 Average-cost Programming
L07 LQ Models
L08 Controllability
L09 Infinite Horizon Models
L10 Observability
L11 Kalman Filtering and Certainty Equivalence
L12 Dynamic Programming in Continuous Time
L13 Pontryagin’s Maximum Principle
L14 Applications of the Maximum Principle
L15 Controlled Markov Jump Processes
L16 Controlled Diffusions
Index

Digressions

I sometimes include a small digression half way through each lecture. Here are some of the overheads I have used for these.
  1. The prisoners' dilemma with repetition and discounting (lecture 3).
  2. The `find the oldest' problem (lecture 4).
  3. The Palasti conjecture, a parking problem (lecture 5).
  4. A self-organizing system (lecture 6).
  5. A repeated game with hidden knowledge (lecture 7).
  6. Black Magic, 9 to 5 (photocopiers, Lecture 8).
  7. Instability of a random access communication channel (aloha, Lecture 9).
  8. Optimal search for a moving target (lecture 10).
  9. The lady's nylon stocking problem (Lecture 12).
  10. An advertising model.

What to know

The files below contain brief summaries of the key results you need to know for each of the three parts of the course, and glossaries of keywords and notation for each part.

summary1.pdf, summary2.pdf, summary3.pdf.

Examples Sheets

There are 3 examples sheets available as pdf files. Model solutions will be handed out following supervisions. Once again, these are available as side-by-side A5: exsheet1.pdf, exsheet2.pdf, exsheet3.pdf, 

Recommended books

  1. Bertsekas, D. P., Dynamic Programming. Prentice Hall, 1987. (Useful for Part I of the course.)
  2. Bertsekas, D. P., Dynamic Programming and Optimal Control, Volumes I and II, Prentice Hall, 1995. (Useful for all parts of the course.)
  3. Hocking, L. M., Optimal Control: An introduction to the theory and applications, Oxford 1991. (Chapters 4-7 are good for Part III of the course.)
  4. Ross, S., Introduction to Stochastic Dynamic Programming. Academic Press, 1983. (Chapters I-V are useful for Part I of the course.)
  5. Whittle, P., Optimization Over Time. Volumes I and II. Wiley, 1982-83. (Chapters 5, 17 and 18 of volume I are useful for Part II of the course. Chapter 7, volume II is good for Part III of the course.)

Exam questions

Here are past tripos questions 1995-2006: tripos.pdf

Other items of interest

Here is what the Occupational Outlook Handbook says about careers in operations research.

Here is the home page of INFORMS, the Institute for Operations Research and the Management Sciences.

My fun page.

University of Cambridge > Mathematics > Statistical Laboratory > Richard Weber
Richard Weber ( rrw1@cam.ac.uk )

Last modified: 08 October 2008