Optimization and Control

picture of broom balancing

Course information

This is a home page of resources for Richard Weber's course of 16 lectures to third year Cambridge mathematics students in winder 2016, starting January 14, 2016 (Tue/Thu @ 11 in CMS meeting room 5). This material is provided for students, supervisors (and others) to freely use in connection with this course.

Introduction

This is a course on optimization problems that are posed over time. It addresses dynamic and stochastic elements that were not present in the IB Optimization course, and we consider what happens when some variables are imperfectly observed. Ther are applications of this course in science, economics and engineering (e.g., "insects as optimizers", "planning for retirement", "finding a parking space", "optimal gambling" and "steering a space craft to the moon").

There are no prerequisites, although acquaintance with Probability, Markov chains and Lagrange multipliers is helpful. An important part of the course is to show you a range of applications. The course should appeal to those who liked the type of problems occurring in Optimization IB, Markov Chains IB and Probability IA.

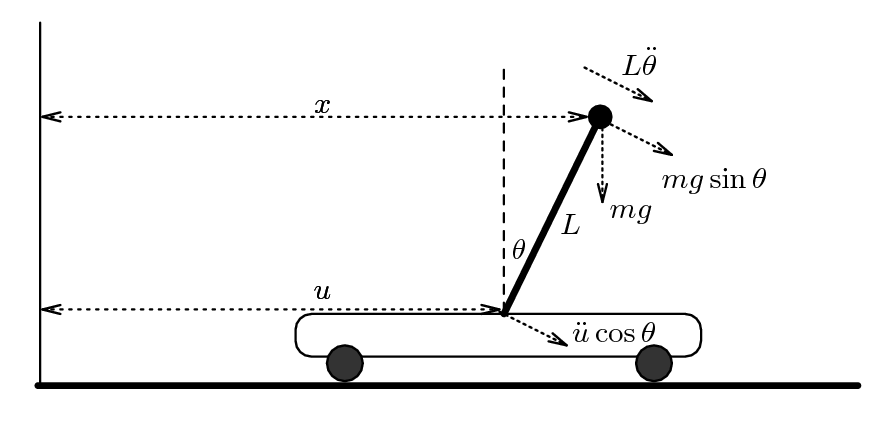
The diagram of the trolley on wheels at the top of this page models the problem that a juggler has when she tries to balance a broom upright in one hand. In this course you will learn how to balance N brooms simultaneously, on top of one another, or perhaps side by side. Can you guess which of these two juggling trick is more difficult mathematically?

Course notes

I aim to make each lecture a self-contained unit on a topic, with notes of four A4 pages.

Here are my draft course notes 2016. These are at present the same as the final course notes 2014. I may make some changes as the course proceeds. You can download a copy now, and take another copy once the course ends.

These notes include:

Table of Contents
Lectures 1 – 16
Slides used in Lecture 7: Multi-armed bandits and Gittins index
Index

The notes contain hyperlinks, but you may not see these in your browser. You will have to download a copy of the pdf file. If you click on an entry in the table of contents, or on a page number in the Index, you will be taken to the appropriate page.

If you find a mistake in these notes, please check that you have the most recent copy (as I may have already made a correction.) Otherwise, please let me know and I will incorporate that correction into the notes.

Course Blog

There is a course blog in which I will make comments after each lecture: to emphasize an idea, give a sidebar, correction (!), or answer an interesting question (perhaps sent by a student in email).

Example Sheets

There are 3 examples sheets, each containing 11 questions, in this single file: exsheetoc.pdf. You should receive a supervision on each examples sheet.

Comments, Discussion and Questions

You can comment or ask questions on the discussion page, and also at the end of each of the blog posts. I will endeavour to answer questions. When you comment, you can do this anonymously if you wish. Just give any name and leave the email address box blank. You can also send me email with questions, suggestions or if you think you have discovered a mistake in the notes.

Feedback

This year's course will finish on Tuesday 2 December 2014. The written feedback questionnaire has been completed by __ students, and a further __ have completed the electronic form. If you have not yet given feedback you can do so using my equivalent on-line form. This will be sent to my email anonymously. After reading the responses, I will forward them to the Faculty Office.

Exam questions

Here is a file of all tripos questions in Optimization and Control for 2001-present.

Here are past tripos questions 1995-2006: tripos.pdf

Some of these questions have amusing real-life applications.

Recommended books

You should be able these books in libraries around Cambridge. Clicking on the title link will show you where the book can be found.

Bertsekas, D. P., Dynamic Programming and Optimal Control, Volumes I and II, Prentice Hall, 3rd edition 2005. (Useful for all parts of the course.) ISBN 1886529086
See also author's web page

Hocking, L. M., Optimal Control: An introduction to the theory and applications, Oxford 1991. (Chapters 4-7 are good for Part III of the course.) ISBN 0198596820

Ross, S., Introduction to Stochastic Dynamic Programming. Academic Press, 1995. (Chapters I-V are useful for Part I of the course.) ISBN 0125984219

Whittle, P., Optimization Over Time. Volumes I and II. Wiley, 1982-83.(Chapters 5, 17 and 18 of volume I are useful for Part II of the course. Chapter 7, volume II is good for Part III of the course.) ISBN 0471101206

Schedules

Dynamic programming
The principle of optimality. The dynamic programming equation for ﬁnite-horizon problems. Interchange arguments. Markov decision processes in discrete time. Inﬁnite-horizon problems: positive, negative and discounted cases. Value interation. Policy improvment algorithm. Stopping problems. Average-cost programming. [6]

LQG systems
Linear dynamics, quadratic costs, Gaussian noise. The Riccati recursion. Controllability. Stabilizability. Inﬁnite-horizon LQ regulation. Observability. Imperfect state observation and the Kalman ﬁlter. Certainty equivalence control. [5]

Continuous-time models
The optimality equation in continuous time. Pontryagin’s maximum principle. Heuristic proof and connection with Lagrangian methods. Transversality conditions. Optimality equations for Markov jump processes and diﬀusion processes. [5]

1 Dynamic Programming
1.1 Control as optimization over time
1.2 The principle of optimality
1.3 Example: the shortest path problem
1.4 The optimality equation
1.5 Example: optimization of consumption
2 Markov Decision Problems
2.1 Markov decision processes
2.2 Features of the state-structured case
2.3 Example: exercising a stock option
2.4 Example: secretary problem
3 Dynamic Programming over the Infinite Horizon
3.1 Discounted costs
3.2 Example: job scheduling
3.3 The operator formulation of the optimality equation
3.4 The infinite-horizon case
3.5 The optimality equation in the infinite-horizon case
3.6 Example: selling an asset
3.7 Example: minimizing flow time on a single machine
3.7.0.1 An interchange argument.
4 Positive Programming
4.1 Example: possible lack of an optimal policy.
4.2 Characterization of the optimal policy
4.3 Example: optimal gambling
4.4 Value iteration
4.5 D case recast as a N or P case
4.6 Example: pharmaceutical trials
5 Negative Programming
5.1 Example: a partially observed MDP
5.2 Stationary policies
5.3 Characterization of the optimal policy
5.3.0.1 The optimality equation.
5.4 Optimal stopping over a finite horizon
5.5 Example: optimal parking
6 Optimal Stopping Problems
6.1 Bruss's odds algorithm
6.2 Example: stopping a random walk
6.3 Optimal stopping over the infinite horizon
6.4 Example: sequential probability ratio test
6.5 Example: prospecting
7 Bandit Processes and the Gittins Index
7.1 Bandit processes and the multi-armed bandit problem
7.2 The two-armed bandit
7.3 Gittins index theorem
7.4 Example: single machine scheduling
7.5 *Proof of the Gittins index theorem*
7.6 Example: Weitzman's problem
7.7 *Calculation of the Gittins index*
7.8 *Forward induction policies*
8 Average-cost Programming
8.1 Average-cost optimality equation
8.2 Example: admission control at a queue
8.3 Value iteration bounds
8.4 Policy improvement algorithm
9 Continuous-time Markov Decision Processes
9.1 Stochastic scheduling on parallel machines
9.2 Controlled Markov jump processes
9.3 Example: admission control at a queue
10 LQ Regulation
10.1 The LQ regulation problem
10.2 The Riccati recursion
10.3 White noise disturbances
10.4 Example: control of an inertial system
11 Controllability
11.1 Controllability
11.2 Controllability in continuous-time
11.3 Linearization of nonlinear models
11.4 Example: broom balancing
11.5 Stabilizability
11.6 Example: pendulum
12 Observability
12.1 Infinite horizon limits
12.2 Observability
12.3 Observability in continuous-time
12.4 Example: satellite in a plane orbit
13 Kalman Filter and Certainty Equivalence
13.1 Imperfect state observation with noise
13.2 The Kalman filter
13.3 Certainty equivalence
13.4 *Risk-sensitive LEQG*
14 Dynamic Programming in Continuous Time
14.1 Example: LQ regulation in continuous time
14.2 The Hamilton-Jacobi-Bellman equation
14.3 Example: harvesting fish
15 Pontryagin's Maximum Principle
15.1 Heuristic derivation of Pontryagin's maximum principle
15.2 Example: parking a rocket car
15.3 PMP via Lagrangian methods
16 Using Pontryagin's Maximum Principle
16.1 Example: insects as optimizers
16.2 Problems in which time appears explicitly
16.3 Example: monopolist
16.4 Example: neoclassical economic growth
16.5 Diffusion processes