Sensitivity Analysis with the $R^2$-calculus
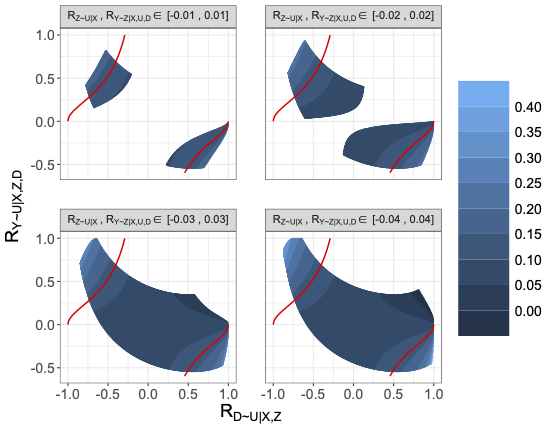 $R$-sensitivity contours for the lower end of the estimated partially identified region
$R$-sensitivity contours for the lower end of the estimated partially identified region
Abstract
Causal inference necessarily relies upon untestable assumptions; hence, it is crucial to assess the robustness of obtained results to violations of identification assumptions. However, such sensitivity analysis is only occasionally undertaken in practice, as many existing methods only apply to relatively simple models and their results are often difficult to interpret. We take a more flexible approach to sensitivity analysis and view it as a constrained stochastic optimization problem. We focus on linear models with an unmeasured confounder and a potential instrument. We show how the $R^2$-calculus—a set of algebraic rules that relates different (partial) $R^2$-values and correlations—can be applied to identify the bias of the $k$-class estimators and construct sensitivity models flexibly. We further show that the heuristic ``plug-in’’ sensitivity interval may not have any confidence guarantees; instead, we propose a boostrap approach to construct sensitivity intervals which perform well in numerical simulations. We illustrate the proposed methods with a real study on the causal effect of education on earnings and provide user-friendly visualization tools.