The origin of randomization
This post is derived from my talk “Fisher, Statistics, and Randomization” in the Fisher in the 21st Century Conference organized by Fisher’s College, Gonville & Caius. In the first half of that talk, I tried to trace the origin of randomization. Fisher is widely credited as the person who first advocated randomization in a systematic manner. In doing so, he profoundly changed how modern science is being done.
My history hunt was largely based on two articles that gave an excellent review of the early history of randomization:
- I. Hacking. (1988). Telepathy: Origins of Randomization in Experimental Design. Isis 79.
- J. F. Box. (1980). R. A. Fisher and the Design of Experiments, 1922–1926. The American Statistician 34.
The organization of my discussion is inspired by David Cox’s synthesis in 2009 that randomization plays three broad roles in the design of experiments:
to avoid selection and other biases and to do so in a publically convincing way,
to provide a unified approach to the second-order analysis of many standard designs, and
to provide a basis for exact tests of significance and related interval estimates.
{{% toc %}}
First role: Avoid bias
The first role, that randomization eliminates unmeasured confounding bias, is the usual rationale used to justify randomization. Ian Hacking gave a thorough historical review of how randomization became adopted in an area of psychology concerning psychophysics.
The first randomized double-blind experiment, according to Stephen Stigler, was done by Charles Sanders Peirce and his student Joseph Jastrow. Peirce is an important American philosopher who founded the philosophical tradition of pragmatism. In a paper titled “On Small Differences in Sensation”, Peirce and Jastrow set out to test the hypothesis that there is (no) threshold in our sensation of pressure. To do so, they ran a series of trials in which experimental subjects first experienced a weight of 1kg and then a second weight either slightly heavier or slightly lighter than the first. For the purpose of this post, the important thing is that whether weight is added or subtracted was determined by well shuffled decks of cards. Peirce and Jastrow indeed had the following to say about this choice of the experimental design:
A slight disadvantage in this mode of proceeding arises from the long runs of one particular kind of change, which would occasionally be produced by chance and would tend to confuse the mind of the subject. But it seems clear that this disadvantage was less than that which would have been occasioned by his knowing that there would be no such long runs if any means had been taken to prevent them.
Around the same time, a French physician, Charles Richet, who ended up winning the Nobel prize in physiology and medicine in 1913 for a different work, used randomized experiments to investigate the possibility that a person can detect weak powers of telepathy. He proposed a long sequence of trials in which an “agent” drew a playing card at random and concentrated upon it for a short time, after which a “reagent” guessed the suit of the card. In 2927 trials, Richet ended up with 789 successes. Hacking mentioned a quantitative analysis of this by Francis Edgeworth. Here is a modern analysis using R.
> binom.test(789, 2927, p = 0.25)
Exact binomial test
data: 789 and 2927
number of successes = 789, number of trials = 2927, p-value = 0.01497
alternative hypothesis: true probability of success is not equal to 0.25
95 percent confidence interval:
0.2535501 0.2860304
sample estimates:
probability of success
0.2695593
As we can see, the two-sided p-value is about 0.015 and the point estimate is slightly above 0.25—the expected probability for random guessing.
Hacking then reviewed critiques of Richet’s experiment and subsequent development. He described a similar experiment design adopted by John Coover in 1912, a psychologist in Stanford, in which several steps of the experiment were randomized, including whether the subject is “treated” (the agent actually looked at the card) or “control” (the agent did not look at the card at all).
Given today’s perception of mind and telepathy (or perhaps I should say my perception, as I am not religious), the scientific hypotheses of these experiments may look rather amusing. Hacking, however, gave a good reason for why randomization was first adopted in psychic research:
But suppose we turn to a subject about which nothing whatsoever is known, so that one cannot even begin to speculate intelligently about causes of variation? Suppose, further, that it is a subject redolent of fraud, an activity that even Bayesians admit can be controlled for by randomization? That is where we should be looking: psychic research. The more “empirical” and nontheoretical a question, the more randomization makes sense.
At the end of his article, Hacking commented that Fisher was well aware of this line of work, but Fisher thought it was “baloney”. Hacking wrote: “He knew of this kind of work, but a very different level of sophistication was involved in Fisherian randomization”. Based on similar evidence, Trudy Toady reached a different conclusion:
I argue… that the random group design was advanced in psychology before Fisher introduced it in agriculture and that in this context it was the unplanned outcome of a lengthy historical process rather than the instantaneous creation of a single genius.
This was later criticized by Nancy Hall, who argued forcefully that Fisher’s conception of randomization was larged based on his geometric intuition. This is indeed the subject of discussion in our next section. To end this section, I want to give a pointer to an article titled “Statistical Problems in ESP Research” from Persi Diaconis, who was the lecturer of my first measure-theoretic probability course in Stanford.
Second role: Justification of statistical inference
Fisher’s main argument for using randomization is that it justifies the standard linear model analysis of experimental data. As argued by Joan Fisher Box, Fisher’s daughter and biographer, and Nancy Hall, Fisher’s conception of randomization was rooted in his geometric intuitions. This can be traced back to Fisher’s study of small sample statistics. and correspondence with William Gosset (aka “Student”) since 1912; the friendship between Fisher and Gosset is reviewed in another paper by Box. Being employed as a brewer at Guinness’s Brewery, Gosset needed a way to estimate the accuracy of sample mean and correlation coefficient and conjectured their sampling distributions in two publications in 1908 by calculating their first four moments. Fisher gave a rigorous derivation of Gosset’s result in 1915. Here is what Fisher wrote:
This result, although arrived at by empirical methods, was established almost beyond reasonable doubt in the first of “Student’s” papers. Is it, however, of interest to notice that the form establishes itself instantly, when the distribution of the sample is viewed geometrically.
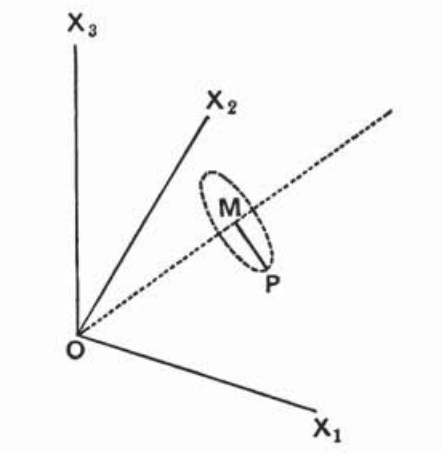
Fisher then described his geometric intuition using the illustration above with \(n=3\) observations. His argument involved representing a vector of \(n\) observations \((x_1,\dotsc,x_n)\) as a point \(P\) in the $n$-dimensional space. Let \(\bar{x} = \sum_{i=1}^n x_i/n\) be the sample mean and \(\mu_1 = \sum_{i=1}^n (x_i - \bar{x})^2/n\) (notice that Fisher used \(n\) as the divisor in this sample variance). Fisher wrote: “For, given \(\bar{x}\) and \(\mu_1\), \(P\) must lie on a sphere in \(n-1\) dimensions.” As pointed out by Hall (p. 308), Fisher repeatedly used this geometric discussion in several problems later on.
After being appointed as a statistician at the Rothamsted Experimental Station in 1919, Fisher started to connect this geometric idea with randomization. In his 1923 paper with MacKenzie where the analysis of variance table appeared for the first time, Fisher wrote:
If all the plots are undifferentiated, as if the numbers had been mixed up and written down in random order, the average value of each of the two parts [of the sum of squares] is proportional to [their] number of degrees of freedom [, respectively].
In his 1926 paper in which the role of randomization was first elaborated on, Fisher wrote:
One way of making sure that a valid estimate of error will be obtained is to arrange the plots deliberately at random, so that no distinction can creep in between pairs of plots treated alike and pairs treated differently; in such a case an estimate of error, derived in the usual way from the variations of sets of plots treated alike, may be applied to test the significance of the observed difference between the averages of plots treated differently.
So it is clear that besides the usual argument that randomization eliminates unmeasured bias, Fisher’s main point is that randomization ensures correct uncertainty quantification, without the assumption of normality. Box described Fisher’s intuitive reasoning as follows.
His confidence in the result, however, depended on the geometric representation that was by then second nature to him. He could picture the distribution of n results as a pattern in n- dimensional space, and he could see that randomization would produce a symmetry in that pattern rather like that produced by a kaleidoscope, and which approximated the required spherical symmetry available, in particular, from standard normal theory assumptions.
However, what Fisher precisely had in mind is still a mystery (at least to me). In the standard theory for analysis of variance, a key enabling result is that \(\|\mathbf P \mathbf Y\|^2 \sim \chi^2_{\text{tr}(\mathbf P)}\), where \(\mathbf P\) is a projection matrix, \(\mathbf Y \sim \mathrm{N}(\mathbf 0, \mathbf I)\) is standard normal, and \(\text{tr}(\mathbf P)\) is the trace of \(\mathbf P\). Fisher must have seen that such a result is approximately true if \(\mathbf Y\) is in some sense randomized. But some conditions on the randomization seem necessary. For example, \(\mathbb{E}[\|\mathbf P \mathbf Y\|^2] = \text{tr}\{\mathbf P \, \text{Cov}(\mathbf Y)\}\). So it seems necessary that \(\text{Cov}(\mathbf Y) \propto \mathbf I\) (identity matrix) in the randomization distribution. This would almost, but not precisely, hold for the permutation distribution. The connection between the normal theory distribution and the randomization distribution was not formally established until Kempthorne’s work in 1955 by requiring ``additivity’’ (treatment effect is homogeneous)
Third role: Physical basis for randomization tests
Fisher first described randomization tests in his classic book Design of Experiments in 1935 (p. 45):
There has … been a tendancy for theoretical statisticians, not closely in touch with the require- ments of experimental data, to stress the element of normality, …, as though it were a serious limitation to the test applied. In these discussions it seems to have escaped recognition that the physical act of randomisation, …, affords the means of examining the wider hypothesis in which no normality of distribution is implied.
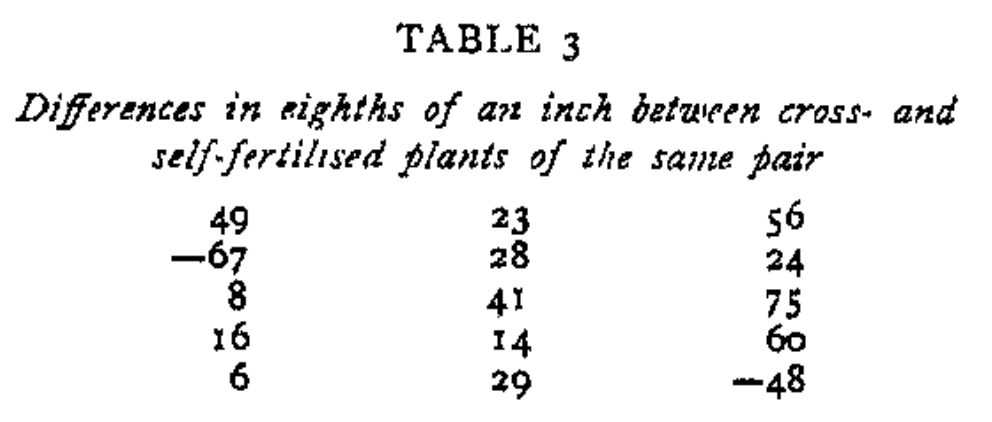
Fisher then demonstrated how randomization can be used to construct a test using the above example of a pariwise randomized experiment. He wrote (p. 45-46):
Their sum, taking account of the two negative signs which have actually occurred, is 314, and we may ask how many of the 215 numbers, which may be formed by giving each component alternatively a positive and a negative sign, exceed this value.
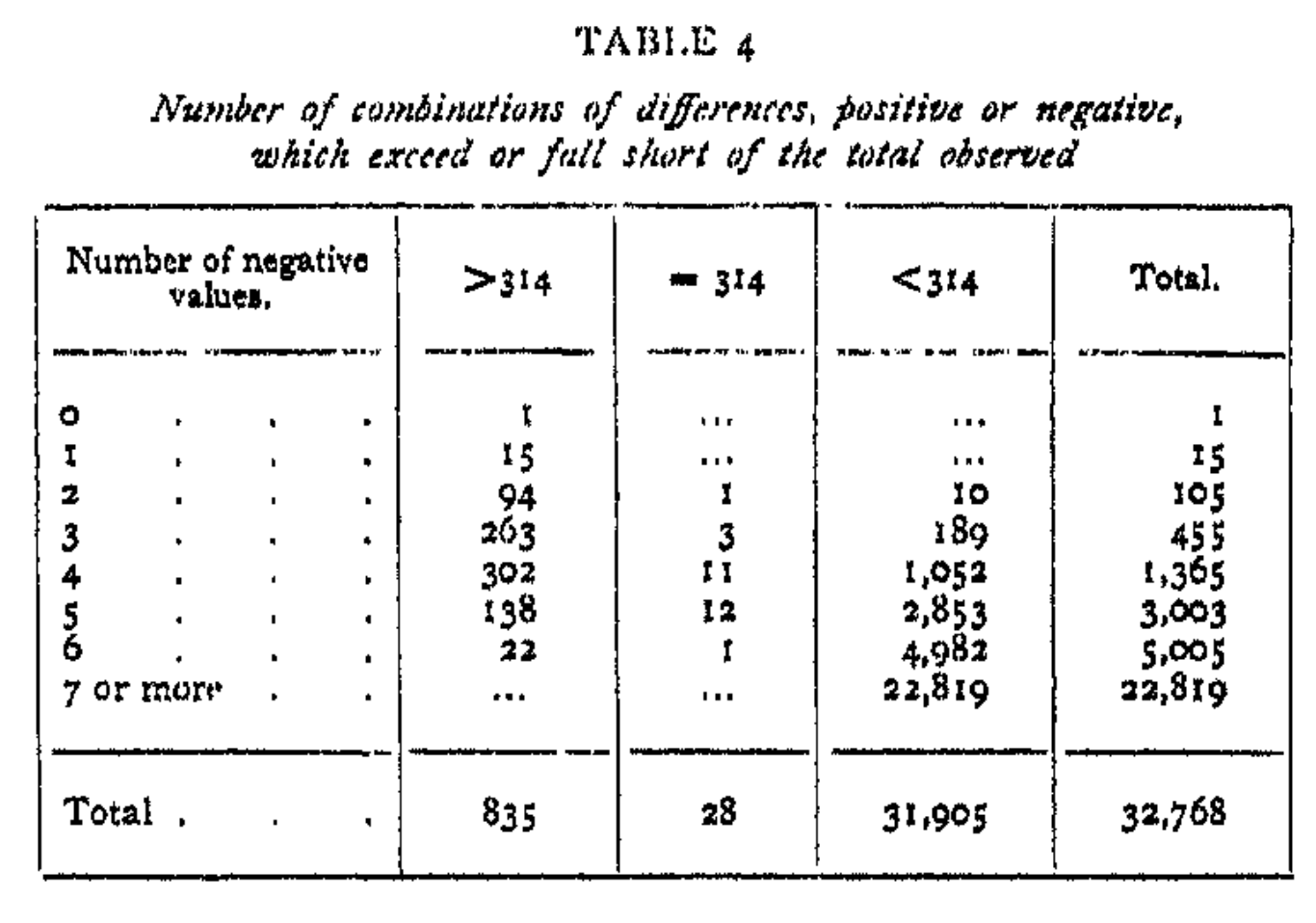
Fisher then found the table above to find that the randomization p-value is \((835 + 28)/32768 \times 2 \approx 0.053\), which is very close to the p-value of a t-test. He mainly used this to justify the application of the usual t-test that is based on the normality assumption. Fisher’s idea was immediately extended by Pitman, Welch, and many others, who emphasized on the model-free or nonparametric nature of such tests. Fisher, however, was not very positive about them in his 1960 revision of the book (Sec. 21.1):
In recent years tests using the physical act of randomisation … have been largely advocated under the name of ``Non-parametric’' tests. Somewhat extravagant claims have often been made on their behalf. …
They assume less knowledge, or more ignorance, of the experimental material than do the standard tests, and this has been an attraction to some mathematicians who often discuss experimentation without personal knowledge of the material. In inductive logic, however, an erroneous assumption of ignorance is not innocuous; it often leads to manifest absurdities.
This prompted Basu (1980) to suggest that Fisher has retracted his support of the randomization tests (I received exactly this same comment during the conference). I tend to agree with the comments by Kempthorne and Rubin that Basu overinterpreted Fisher’s intention. Fisher’s criticism was mainly towards the “extravagant claims” made about nonparametric tests, in which physical randomization is typically replaced by the theoreical assumption of repeated sampling from the same distribution (or some weaker forms of exchangeability). Given Fisher’s pragmatic attitude towards applications, I would be surprised if he objects the usage of randomization tests when the normality assumption is clearly not satisfied. A good example of this is Fisher’s exact test for \(2 \times 2\) tables, which is a randomization test; see this recent paper of mine.
Interplay between genetics and statistics
One interesting angle that often gets ignored in discussions of the origin of randomization is the interplay between Fisher’s work in genetics and statistics. The most notable examples were the use of “variance”" and the development of factorial experimental designs; see Bodmer (2003). In Fisher’s famous 1918 genetics paper “The correlation between relatives on the supposition of Mendelian inheritance”, he wrote:
It is therefore desirable in analysing the causes of variability to deal with the square of the standard deviation as the measure of variability. We shall term this quality the Variance of the normal population to which it refers, and we may now ascribe to the constituent causes fractions or percentages of the total variance which they together produce.
In the 1951 Bateson lecture, Fisher revealed the origin of the factorial design of experiment:
And here I may mention a connection between our two subjects which seems not to be altogether accidental, namely that the “factorial” method of experimentation, now of lively concern so far afield as the psychologists or the industrial chemists, derives its structure, and its name, from the simultaneous inheritance of Mendelian factors.
I did not find any discussion of this, but it is not unreasonable to postulate that the origin of randomization in Fisher’s thinking was seeded in his understanding of Mendelian genetics. George Davey Smith pointed me to the following two articles. In a retrospect of Fisher’s life, George Barnard in 1990 made an insightful connection between Mendelian genetics and frequentist statistics:
Mendel’s theory was the first in natural science to express its experimental predictions in terms of exact frequency probabilities—for example that the probability that a pea from a certain type of cross will be round rather than wrinkled is 3/4-not approximately 0.75, but 3/4. … But the idea that nature itself could behave like a perfect gambling machine was revolutionary.
Moreover, Fisher clearly knew the natural randomization in heredity. In his Bateson lecture, he wrote
Genetics is indeed in a peculiarly favoured condition in that Providence has shielded the geneti- cist from many of the difficulties of a reliably controlled comparison. The different genotypes possible from the same mating have been beautifully randomised by the meiotic pro- cess. A more perfect control of conditions is scarcely possible, than that of different genotypes appearing in the same litter.
If we compare Fisher with the psychologists before him, with Bradford Hill who strongly advocated for randomized clinical trials, or with Jerzy Neyman who gave the first randomization-based analysis in his 1923 thesis, Fisher stands apart by his emphasis of how physical randomization justifies statistical inference and his deep understanding of genetics. So as others may saw randomization as a possibly artificial adjunct to experiments, the idea of randomization would be a second instinct to Fisher as he knew how nature randomizes all the time in evolution better than any of his peers.
I suppose we will never know the answer to my speculation here, but it is extremely revealing to consider how Fisher’s interest in genetics and statistics interacted. The modern research area “Mendelian randomization” exactly builds on the natural experiment in heredity; see this recent review article by Pingault, Richmond, and Davey Smith and this page which contains my work in this area.
Randomization without Fisher
At the end of my talk, I speculated that without Fisher, the modern practice of randomized experiments and clinical trials could have been delayed by decades. This was of course a speculation of a counterfactual that we will never know, but it was based on two good considerations. First, Fisher had a quite unique combination of skills—geometry, statistics, and mathematical genetics, and he was employed by the Rothamsted Experimental Station to think about agricultural experiments. That looks like a very extraordinary situation which might not happen frequnetly. Second, Fisher had the strong personality required to push forward randomization—a revolutionary and unintuitive idea. He did it so well that we take the idea for granted today, but we should not underestimate the intellectual brilliance behind.
Update: Hyunseung Kang pointed me to this paper by Freedman and Lane that seems to clarify Fisher’s “geometric intuition” about randomization/permutation to some extent.