Modelling Communication Networks Frank Kelly University of Cambridge
Robert Clayton
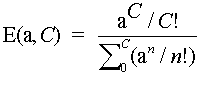
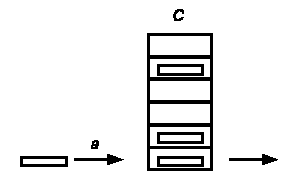
Link constraint
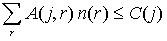
> C frequencies in total: reuse possible in non-adjacent cells
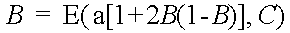
Two principles:
Analytical (black) and simulated (grey)
(USA busy hour)
(European busy hour)
Define the value of a coalition S to be:
V(S) = [cost separate] - [cost with coalition S]
| Subset S | Separate | Coalition | V(S) | Saving |
|---|---|---|---|---|
|
UK,USA,J A,UK,USA F,J,USA A,F,USA UK,C,J A,UK,C |
13895 12610 6904 5600 3995 3869 |
11134 10406 5609 4801 3199 3127 |
2761 2204 1295 799 796 742 |
20% 17% 19% 14% 20% 19% |
| Subset S | Separate | Coalition | V(S) | Saving |
|---|---|---|---|---|
|
A,J,UK,USA F,J,UK,USA A,F,J,USA C,J,UK,USA |
18558 20248 18847 15860 |
13573 16733 15982 13044 |
4985 3515 2865 2816 |
27% 17% 15% 18% |
|
A,F,J,UK,USA A,C,J,UK,USA |
24990 20667 |
19188 15570 |
5802 5097 |
23% 25% |
The core is the set of vectors (x(i), i a player) satisfying:
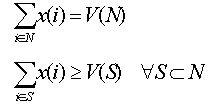
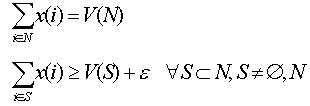
The least core is the smallest epsilon-core
| A | F | J | UK | USA | Winner |
|---|---|---|---|---|---|
| 409 | 409 | 2528 | 409 | 2048 | J,USA |
| 409 | 409 | 2528 | 2048 | 409 | J,UK |
| 1877 | 409 | 886 | 2221 | 409 | A,UK |
| 1877 1877 | 409 409 | 2528 2528 | 409 579 |
579 409 | A,J A,J |
| 429 409 | 409 409 | 886 906 | 3670 3670 |
409 409 | UK UK |
| Shapley values | |||||
| 826 | 415 | 1076 | 1479 | 2003 | |
3 hours: Time unit - 10 seconds
17 minutes: Time unit - 1 second>
2 minutes: Time unit - 0.1 seconds
10 seconds: Time unit - 0.01 seconds
Black case:
60 sources with peak 1 and mean 0.5
15 sources with peak 4 and mean 1.0
These two cases have
Two major issues:
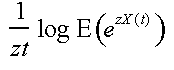
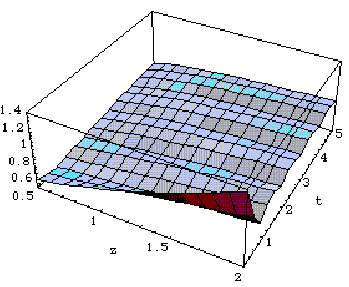
As z increases, the effective bandwidth increases from the mean to the maximum of X(t)/t

Issues: